七、OpenGL——变化

1 数学知识

1.1 单位矩阵

在OpenGL中，由于某些原因我们通常使用4×4的变换矩阵，而其中最重要的原因就是大部分的向量都是4分量的。我们能想到的最简单的变换矩阵就是单位矩阵(Identity Matrix)。单位矩阵是一个除了对角线以外都是0的N×N矩阵。在下式中可以看到，这种变换矩阵使一个向量完全不变：

注意：向量在矩阵的右侧

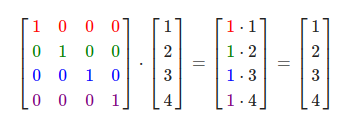
alt text

1.2 缩放

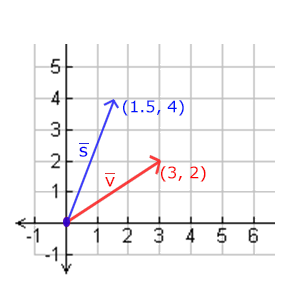
对(x, y)坐标继续缩放，比如x轴坐标缩小一半，y轴坐标放大一倍，向量v¯缩放后s¯如图所示：

alt text

上面这种缩放操作是不均匀缩放，因为每个轴的缩放因子不一样。如果每个轴的缩放因子都一样那么就叫均匀缩放。

如果我们把缩放变量表示为(S1,S2,S3)，我们可以为任意向量(x,y,z)定义一个缩放矩阵：

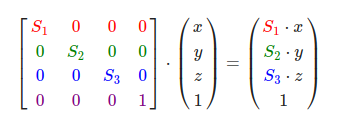
alt text

注意，第四个缩放向量仍然是1，因为在3D空间中缩放w分量是无意义的。w分量另有其他用途，在后面我们会看到。

1.3 位移

位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程，从而在位移向量基础上移动了原始向量。我们已经讨论了向量加法，所以这应该不会太陌生。

和缩放矩阵一样，在4×4矩阵上有几个特别的位置用来执行特定的操作，对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz) ，我们就能把位移矩阵定义为：

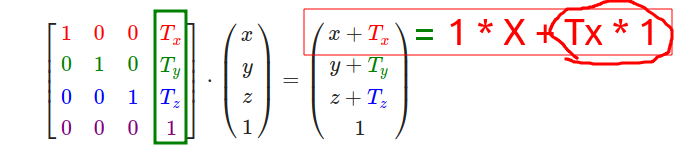
alt text

向量（x，y，z，w）如果没有w行，位移值就没有地方可乘可加了。

alt text

1.4 旋转

在3D空间中旋转需要定义一个角和一个旋转轴(Rotation Axis)。物体会沿着给定的旋转轴旋转特定角度。

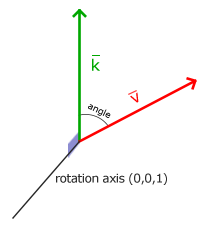
alt text

旋转矩阵需要指定旋转轴(Rx,Ry,Rz)和旋转角度 θ。

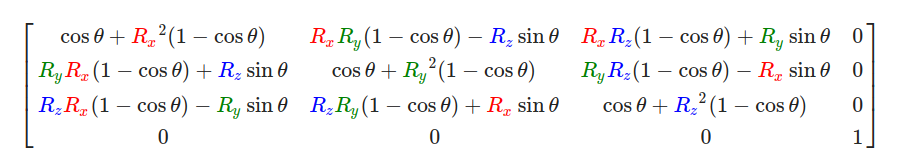
alt text

1.5 矩阵的组合

矩阵的乘法是不遵守交换律的，这意味着它们的顺序很重要。在最后边的矩阵是第一个与向量相乘的，所以你应该从右向左读这个乘法。

所以建议：

先进行缩放操作。
进行旋转操作。
最后再进行位移操作。

trans = 位移 x 旋转 x 缩放

2 实践

我们已经了解了背后的所有理论，OpenGL没有自带任何的矩阵和向量知识，所以我们必须定义自己的数学类和函数。幸运的是，有个易于使用，专门为OpenGL量身定做的数学库，那就是 GLM。

GLM是OpenGL Mathematics的缩写，它是一个只有头文件的库，也就是说我们只需包含对应的头文件就行了，不用链接和编译。GLM可以在它们的网站上下载。把头文件的根目录复制到你的includes文件夹，然后你就可以使用这个库了。

GLM库从0.9.9版本起，默认会将矩阵类型初始化为一个零矩阵（所有元素均为0），而不是单位矩阵（对角元素为1，其它元素为0）。所以需要初始化：

glm::mat4 mat = glm::mat4(1.0f)

glm库下载链接：https://github.com/g-truc/glm

下载编译完成后，复制头文件和库文件到相应路径。

头文件夹路径：/assets/OpenGL/glm/

库文件夹路径：/assets/OpenGL/lib/

2.1 glm小练习

我们来看看是否可以利用我们刚学的变换知识把一个向量(1, 0, 0)位移(1, 1, 0)个单位。

#include "glm/glm.hpp"
#include "glm/gtc/matrix_transform.hpp"
#include "glm/gtc/type_ptr.hpp"
#include <iostream>


int 
main(int argc, char const *argv[]) {

  /* 新建一个向量变量 vec，该向量齐次坐标设定为 1.0 */
  glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
  /* 初始化4x4单位矩阵 */
  glm::mat4 trans = glm::mat4(1.0f);

  /* 通过单位矩阵，创建位移变化矩阵 */
  trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));

  /* 矩阵相乘，此时称号操作符已经重载 */
  vec = trans * vec;

  printf ("(%0.2f, %0.2f, %0.2f)\n", vec.x, vec.y, vec.z);

  return 0;
}

2.2 变化顶点

修改顶点着色器，让其接收一个 mat4 的uniform变量，然后再用矩阵uniform乘以位置向量。

 #version 330 core
 layout (location = 0) in vec3 aPos;
 layout (location = 1) in vec2 aTexCoord;

 out vec2 TexCoord;

 uniform mat4 transform;

 void main()
 {
     gl_Position = transform * vec4(aPos, 1.0f);
     TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
 }

我们把箱子放到窗口的右下角(0.5f, -0.5f, 0.0f)，还要让箱子随着时间推移随着Z轴旋转。

 glm::mat4 trans;
 trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
 trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

记住，实际的变换顺序应该与阅读顺序相反：尽管在代码中我们先位移再旋转，实际的变换却是先应用旋转再是位移的。明白所有这些变换的组合，并且知道它们是如何应用到物体上是一件非常困难的事情。只有不断地尝试和实验这些变换你才能快速地掌握它们。

实际：先缩放，再旋转，最后位移操作。

代码：trans = 位移 x 旋转 x 缩放

具体代码查看：07_transformations.cpp

3 练习

3.1 练习一

使用应用在箱子上的最后一个变换，尝试将其改变为先旋转，后位移。看看发生了什么，试着想想为什么会发生这样的事情。

trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));    

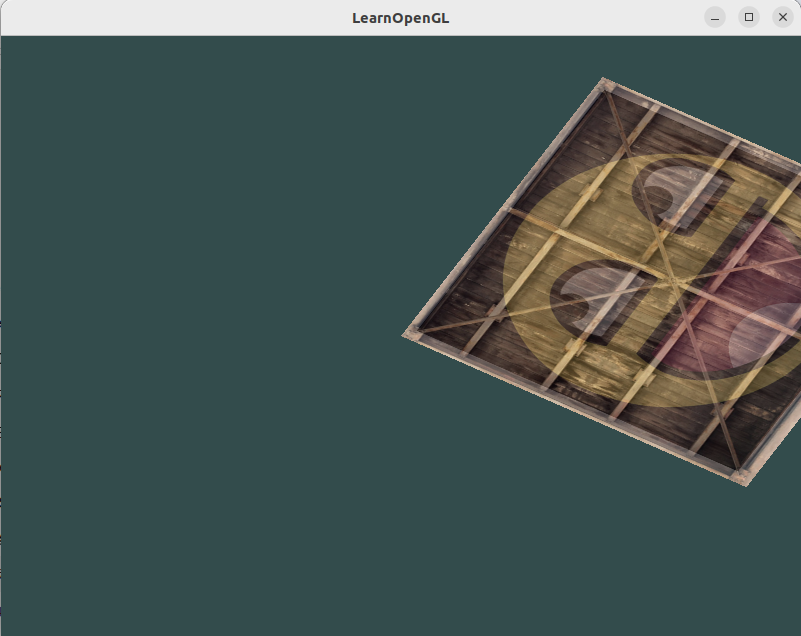
alt text

不难发现，原先由绕着箱子中心旋转，变成了绕着未被位移时候箱子的中心旋转。这是因为 trans = 旋转 * 位移，先进行位移，然后才对其旋转，所以旋转的中心并没有被进行位移。

3.2 练习二

尝试再次调用glDrawElements画出第二个箱子，只使用变换将其摆放在不同的位置。让这个箱子被摆放在窗口的左上角，并且会不断的缩放（而不是旋转）。（sin函数在这里会很有用，不过注意使用sin函数时应用负值会导致物体被翻转）

alt text

答：画第一个箱子的时候变化矩阵trans为单位矩阵，再画第二次的时候修改trans即可。